Métodos

Para el análisis de los núcleos teñidos de marrón en las imágenes para un paciente y una subregión dados, se aplican distintos métodos, funciones y técnicas implementados en python. Para la elección y validación de ciertos métodos (como por ejemplo la decisión de utilizar Otsu thresholded) se utilizó también el programa Fiji de ImageJ.

Análisis en distintos espacios de color

Tomando diferentes espacios de color, se observa que tomando el canal a del espacio Lab se puede diferenciar en mayor medida los núcleos de color marrón del resto. Esto puede verse también tomando los histogramas para cada canal en cada espacio de color. Los tres parámetros en el modelo Lab representan la luminosidad de color L, donde L = 0 indica menor y L = 100 indica mayor luminosidad, su posición entre rojo y verde a, donde valores negativos indican más verde y valores positivos indican más rojo y su posición entre amarillo y azul b, donde valores negativos indican más azul y valores positivos indican más amarillo.

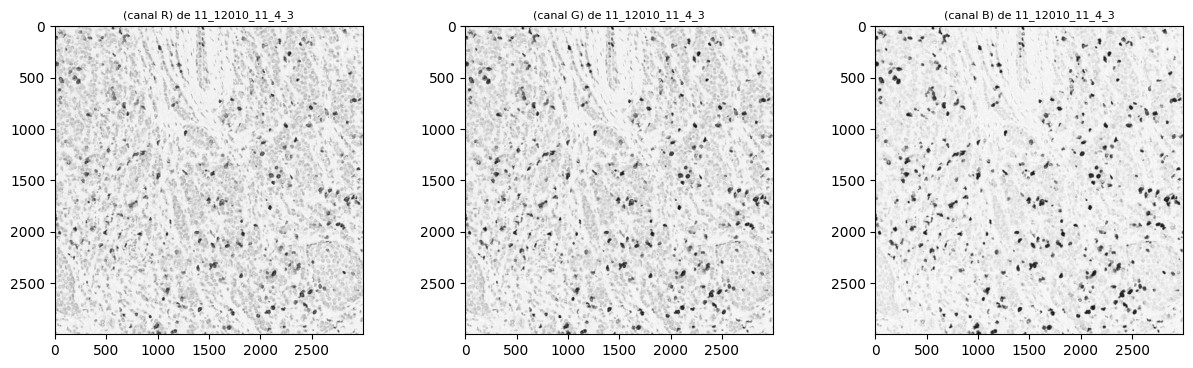
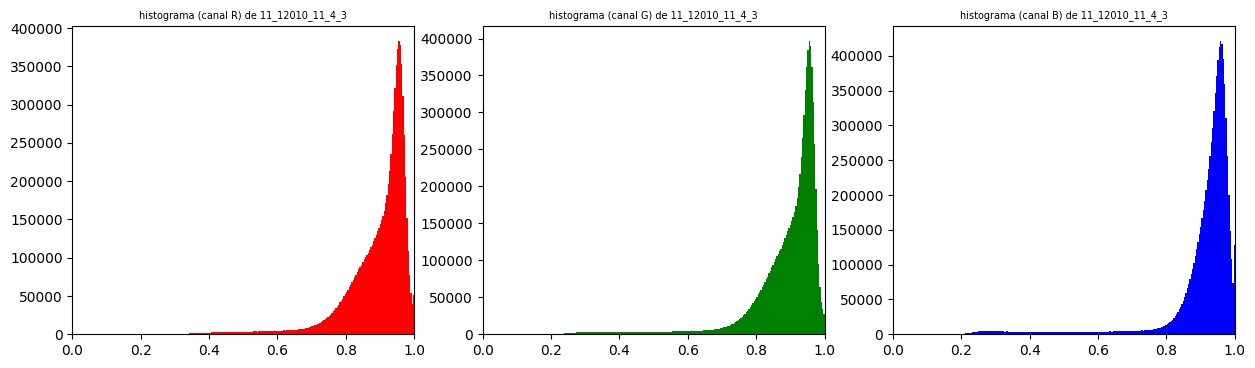
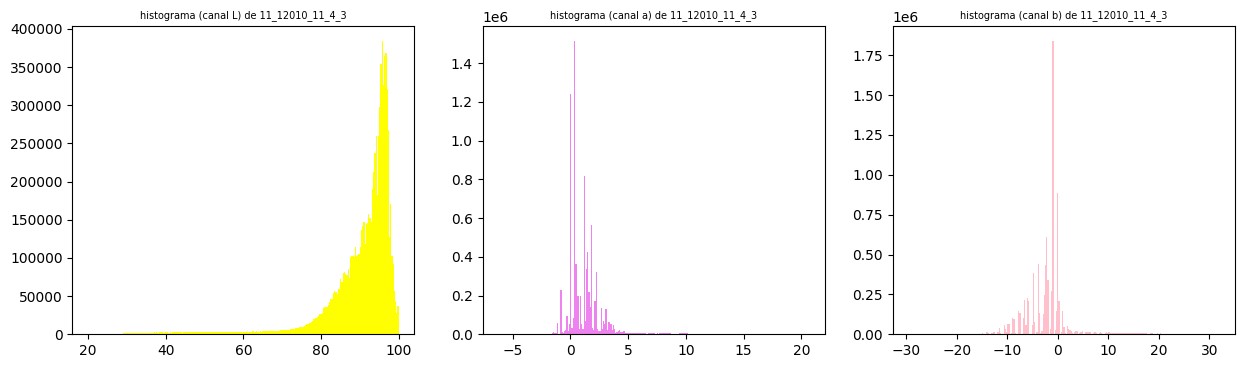
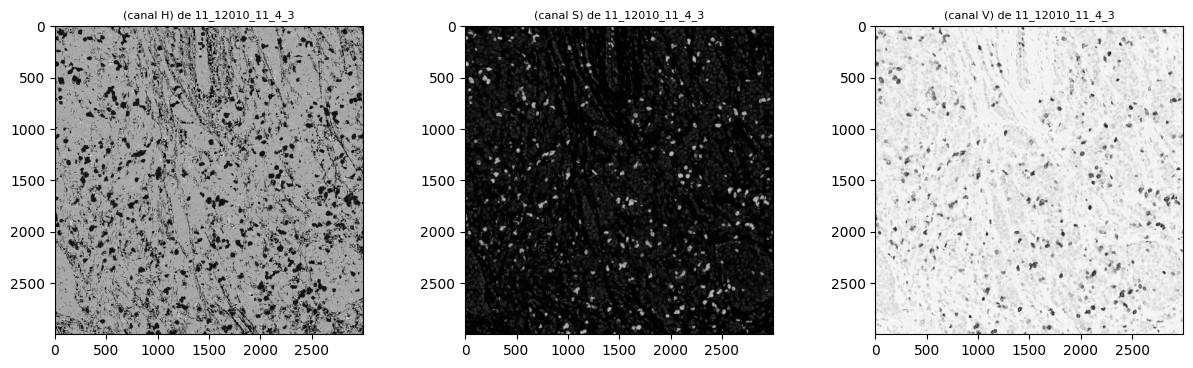
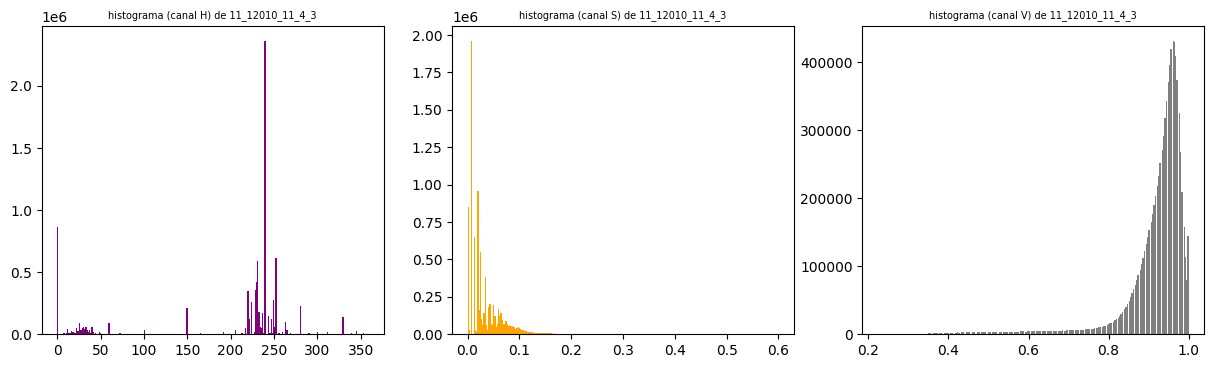
En las figuras 1, 2 y 3 se pueden observar para una misma imagen los tres canales para los espacios de color RGB, Lab y HSV respectivamente, con sus correspondientes histogramas. Una vez que se tiene el canal a del espacio de color Lab, se procede a realizar una umbralización de la imagen. Para ello, tras realizar pruebas con distintas técnicas de umbralización, se opta por implementar el algoritmo de Otsu.

Umbralización

El algoritmo de Otsu, llamado así en honor a Nobuyuki Otsu que lo inventó en 1979, es una técnica de umbralización automática. Utiliza la varianza, que es una medida de la dispersión de valores (en este caso se trata de la dispersión de los niveles de gris). El objetivo es determinar un valor de umbral óptimo para dividir una imagen en dos clases: píxeles de primer plano (Foreground) y píxeles de fondo (Background) de manera que se minimice la 'intra-class variance' de las clases. A partir del histograma de la imagen, se itera sobre distintos valores de umbral y se calcula la varianza entre clases. La idea es determinar el valor umbral de forma que la dispersión dentro de cada clase sea lo más pequeña posible, pero al mismo tiempo la dispersión sea lo más alta posible entre clases diferentes.

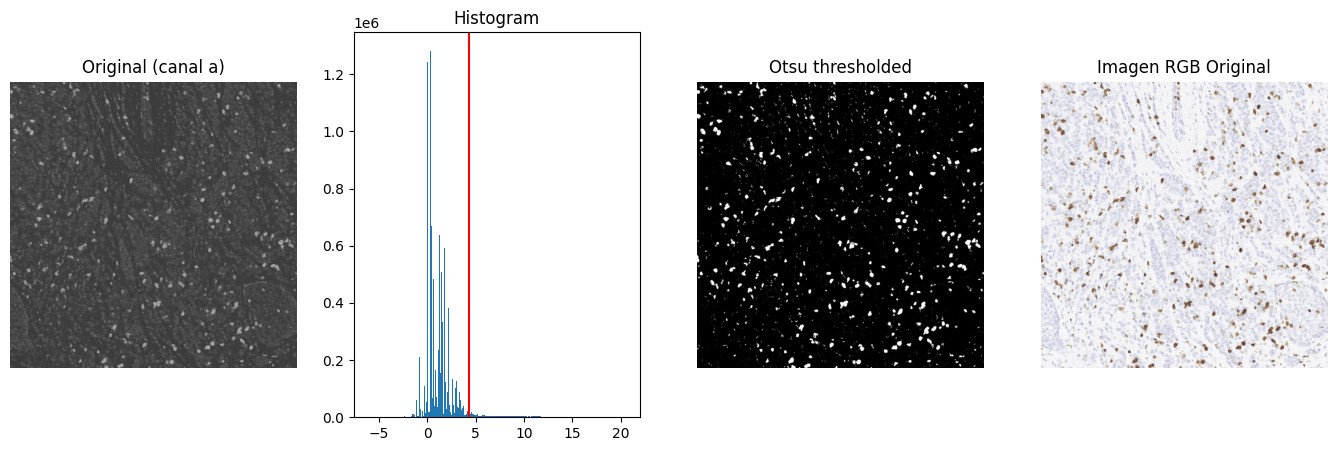
En la figura 4 se tiene por ejemplo para una imagen el umbral hallado mediante el algoritmo de Otsu y la imagen binarizada que se obtiene aplicando dicho umbral.

Transformaciones morfológicas

Una vez obtenido el valor de umbral óptimo (para esa imagen en particular), se realiza una apertura, para eliminar objetos pequeños y líneas finas de la imagen binarizada pero intentando conservar la forma y el tamaño de los objetos más grandes de la imagen. Debido a la forma que presentan los núcleos que se desean determinar, se decide utilizar como elemento estructurante B un kernel de forma elíptica.

En la figura 5 se observan las imágenes tras realizar la apertura. La operación de apertura morfológica consiste en una erosión seguida de una dilatación utilizando el mismo elemento estructurante para ambas operaciones.

Etiquetado y conteo de núcleos teñidos

Tras la apertura, se realizó un etiquetado (utilizando conectividad 8) y luego contando la cantidad de regiones distintas detectadas.

Para el etiquetado, dada una imagen binaria se desea obtener una lista de listas de píxeles conexos (regiones). En nuestro caso deseamos contar cuántas regiones distintas se detectan en la imagen. Brevemente, el algoritmo de etiquetado de componentes conexas consiste en realizar dos pasadas por la imagen. Un primer paso analizando cada píxel y asignándole una etiqueta en base a los píxeles en su vecindad (para definir si dos píxeles son vecinos debe elegirse con qué conectividad estamos trabajando, por ejemplo conectividad 4 donde se observan los vecinos a la izquierda y arriba del píxel objetivo, o conectividad 8 donde se analizan los vecinos a la izquierda, diagonal izquierda, arriba y diagonal derecha del píxel objetivo, que es la que finalmente se utiliza en nuestro caso). Luego, en un segundo paso, partiendo de las etiquetas que se le asignó a cada píxel, se forman las regiones o componentes conectadas; se examina cada píxel de la imagen y para cada uno se verifica si su etiqueta es ''raíz'' (es decir, se halla en la cima del árbol de etiquetas de regiones) en la estructura para conjuntos disjuntos, de ser así, se avanza al siguiente paso, ya que la etiqueta del píxel actual tiene el valor más pequeño posible con base a cómo está conectado con sus vecino, pero en caso contrario, recorremos el árbol hasta llegar a la raíz y se reasigna el valor de la etiqueta de dicho píxel al valor de la raíz correspondiente.

Cálculo del porcentaje y comparación de resultados

Una vez obtenido el número de núcleos teñidos de marrón en la imagen (recordemos, estos núcleos son los que reaccionaron frente al antígeno Ki-67, por lo tanto pertenecen a células que se encuentran realizando la mitosis de la proliferación celular, y por lo tanto son posibles células cancerígenas), el porcentaje se calcula dividiendo entre el número total de núcleos presentes en la imagen.

Se realiza también un análisis global para un paciente uniendo toda la información que aportan las imágenes correspondientes a ese paciente, y realizando una categorización acerca de qué procedimientos médicos corresponden para el valor de porcentaje relevado.

Descripción de los núcleos

Para los núcleos teñidos detectados, se buscó adicionalmente caracterizarlos de forma general. Para ello, se calcularon descriptores de región como lo son el área y el perímetro, y se analizó la intensidad media e intensidad máxima que presentaban en la imagen del canal a del espacio de color Lab (que relacionamos con el nivel de marrón que presenta el núcleo en la imagen original). De esta caracterización no se extrae información para determinar el porcentaje de interés, sino que sirve como un aporte extra debido a que los núcleos de células tumorales tienen propiedades morfológicas diferentes a los núcleos de células normales. Principalmente el tamaño del núcleo de la célula respecto al citoplasma es mayor en el caso de células tumorales. El término ''diferenciación celular'' de un tumor es el grado en el que las células cancerosas se asemejan a las células normales, tanto en su apariencia morfológica como en su funcionamiento, mientras que el término ''anaplasia'' hace referencia a la ausencia de diferenciación que conlleva a una falta de especialización o de función celular (usualmente, cuanto menor es la diferencia entre las células cancerígenas y las células normales mayor es su malignidad y más alta es su velocidad de crecimiento).

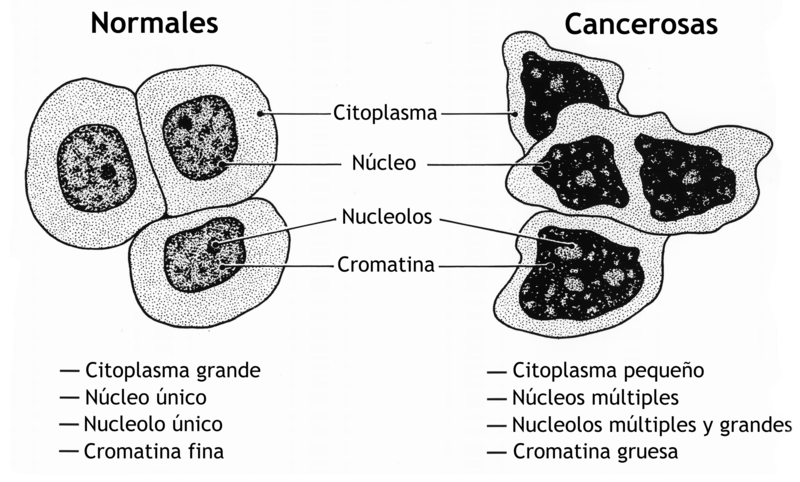
La forma, el tamaño, la composición de proteínas y la textura del núcleo son aspectos y características morfológicas que se ven alteradas en células tumorales (ver figura 6). El núcleo puede adquirir distintos surcos, pliegues o hendiduras, la cromatina puede agregarse o dispersarse y el nucleolo puede agrandarse. En las células normales, el núcleo suele ser de forma redonda o elipsoide, pero en las células cancerosas el contorno suele ser irregular. Diferentes combinaciones de anomalías son características de los diferentes tipos de cáncer, en la medida en que la apariencia nuclear se puede utilizar como marcador en el diagnóstico y la estadificación del cáncer.

Evaluación de desempeño

Dadas las etiquetas, se puede comparar los valores de porcentaje a los que llega nuestro procedimiento con los valores aportados por el conjunto de datos del problema. Para ello, se utilizan varias métricas y técnicas de comparación (por ejemplo, comparación de histogramas).

• Raíz del error cuadrático medio (RMSE): toma la raíz del promedio de los errores al cuadrado, es decir, la diferencia entre el estimador y lo que se estima. Un valor de 0 (casi nunca alcanzado en la práctica) indicaría un ajuste perfecto a los datos.

El RMSE nos da una primera idea del error que presenta nuestro proceso de cálculo de porcentaje.

Adicionalmente, para la validación del desempeño de nuestros procedimientos, basándonos en métricas aplicadas a los histogramas, se utilizan como métricas:

• Correlación - distancia de transporte: es una métrica de similitud entre dos distribuciones de probabilidad, que en el caso discreto puede entenderse como el costo de transporte óptimo para convertir una distribución en la otra. El costo se calcula como el producto de la cantidad de masa de probabilidad que se mueve y la distancia que se mueve. Un valor más chico significa que se mueve una menor cantidad de distancia y de distribución de probabilidad, significando en un menor error.

• Divergencia de Kullback-Leibler: es una medida no simétrica de la similitud o diferencia entre dos funciones de distribución de probabilidad P y Q que mide el número esperado de bits extra requeridos en muestras de código de P cuando se usa un código basado en Q, en lugar de un código basado en P. Se calcula como el promedio ponderado de la diferencia logarítmica entre las probabilidades P y Q, donde el promedio se toma usando las probabilidades P. Un menor valor de divergencia KL significa una aproximación más confiable, mientras que un mayor valor refleja una mayor pérdida de información entre las dos funciones de distribución.

• Entropía cruzada: en teoría de la información, la entropía cruzada entre dos distribuciones de probabilidad mide el número medio de bits necesarios para identificar un evento de un conjunto de posibilidades, si un esquema de codificación está basado en una distribución de probabilidad dada q más que en la verdadera distribución p.